RetroMagazine nr. 44 – Anno: 2023 – Autore: Eugenio Rapella
Il problema delle N regine consiste nel collocare, in una scacchiera quadrata NN, N regine degli scacchi in modo che nessuna di esse minacci una delle altre (la regina degli scacchi minaccia i pezzi che si trovano sulla sua linea, sulla sua colonna o sulle diagonali parallele alle due diagonali della scacchiera). Nel suo “Algoritmi elementari” (un libro davvero splendido), Nicolò Pintacuda propone un codice estremamente sintetico (sono sei istruzioni in Basic!) per il caso classico di una scacchiera 88; il mio contributo consiste in un paio di variazioni in modo che il programma risolva il problema nel caso N*N e venga stampata l’intera scacchiera (e non solo il numero della colonna di posizionamento della regina nelle otto righe).
La tecnica utilizzata è quella del “backtracking”: dopo aver posizionato la prima regina nella prima riga, prima colonna, il programma passa alla riga successiva e una regina viene posizionata in una colonna compatibile con i vincoli del problema. Si continua così; se la colonna non viene trovata, il programma esegue uno o più “passi all’indietro”: modifica la collocazione precedente in modo da sbloccare la situazione e riprende il procedimento. Quando ha posizionato la N-esima regina, il programma stampa la “scacchiera soluzione” e procede alla ricerca di nuove soluzioni. L’arresto avviene quando il programma non può più procedere; in questo caso sono già state stampate tutte le soluzioni (notare che, per N=2 e N=3, il problema non ammette soluzione e dunque non viene stampato nulla).
Il nostro Commodore se la cava con 12 istruzioni, niente male per un problema non proprio banale:
100 print chr$(5):poke 53280,6:input" n = ";n 110 dim dp(2*n-2),ds(2*n),c(n),x(n):k=1:s=1 120 for w=1 to n:a$=a$+chr$(108):b$=b$+chr$(164):next 130 j=j+1:if j<n+1 then if c(j)+ds(j+k)+dp(j-k+n-1) then 130 140 if j>n then k=k-1: goto 210 150 x(k)=j:c(j)=1:ds(j+k)=1:dp(j-k+n-1)=1:if k<n then k=k+1:j=0:goto130 160 print s;"> ";:for t=1 to n: print x(t);: next:print:s=s+1 170 print b$ 180 for t=1 to n 190 print left$(a$,x(t)-1)+chr$(113)+left$(a$,n-x(t))+chr$(165):next 200 print"-------------------------------------":print 210 if k then j=x(k):c(j)=0:ds(j+k)=0:dp(j-k+n-1)=0:goto 130
Alla 100 si imposta il colore dei caratteri (bianco), il colore del bordo (blu) e viene richiesta la dimensione della scacchiera (N); alla 110 si procede alle inizializzazioni e ai dimensionamenti di rito (ci torneremo).
Alla 120 si preparano due stringhe che servono per la stampa della scacchiera: A$ è costituita da una sequenza di N simboli CHR$(108) (una specie di L maiuscola: ∟), B$ è formata da N simboli CHR$(164) (si tratta dell’underscore: _ ). Stampando B$,A$,A$, … , A$ si ottiene la quadrettatura della scacchiera.
Il programma vero e proprio inizia alla 130. J conterrà il numero della colonna, K il numero della riga della casella oggetto dell’analisi; entrambe queste variabili saranno comprese tra 1 e N. Nel Basic del C64, una variabile numerica che non viene inizializzata, vale 0, per cui la prima volta che viene eseguita l’istr. 130 la variabile J assume il valore 1. Stesso discorso vale per i vettori DP(..), DS(..), C(..), X(..) che, all’inizio, sono tutti nulli.
Per descrivere come lavora il programma, consideriamo il caso classico N=8; il significato del vettore X è questo: se X(ALFA)=BETA significa che nella riga ALFA c’è una regina nella colonna BETA. Così, se X(..)=1,3,0,0,0,0,0,0, nelle prime due righe sono posizionate (legalmente) due regine rispettivamente nelle colonne 1 e 3.
Il ruolo dei vettori C(..), DP(..) e DS(..) risulta più chiaro se continuiamo con l’analisi di questa situazione intermedia: una regina è posizionata nella casella (1,1), una regina nella (2,3). Supponiamo che il programma stia valutando la successiva posizione lecita, ovvero una regina in (3,5). In questo momento è K=3 e J=5. Per occupare una posizione riconosciuta lecita entra in gioco l’istruzione 150: X(K)=J, ovvero X(3)=5 – nella terza riga la regina è posizionata in quinta colonna -; C(J)=1, ovvero C(5)=1 la quinta colonna viene “impegnata”.
Ora vanno segnalate come “impegnate” le caselle della diagonale principale (quella parallela alla diagonale che unisce le caselle (1,1) e (8,8)) e quelle della diagonale secondaria (parallela a quella passante per (1,8) e (8,1)).
La diagonale principale relativa alla casella (3,5) è costituita dalle caselle (1,3), (2,4), (3,5), (4,6), (5,7) e (6,8) ed è identificata dalla differenza J-K che, nel nostro esempio, vale -2.
Al vettore DP(..) il compito di segnalare che quella diagonale principale risulta ora impegnata: DP(J-K)=1 (1=impegnata, 0=libera). Nel caso N=8, le differenze J-K vanno da -7 (J=1, K=8) a +7 (J=8, K=1); per evitare indici negativi, sommeremo +7 all’indice in modo che si vada da DP(0) a DP(14). Si spiega ora la DIM DP(2N-2) nella 110 (infatti, per N=8 si ottiene appunto DIM DP(14)) e l’istruzione DP(J-K+N-1)=1 nella 150 (infatti per N=8 è N-1=+7). Un discorso analogo vale per la diagonale secondaria che, in relazione alla casella (3,5), è formata dalle posizioni (1,7), (2,6), (3,5), (4,4), (5,3) (6,2) e (7,1) ed è dunque identificata dall’indice J+K, nel nostro caso pari a 8. Dunque l’assegnazione DS(J+K)=1 nella 150 sta ad indicare che la diagonale in questione risulta impegnata. Poiché gli indici di linea e colonna vanno da 1 a N, J+K raggiunge il valore N+N e questo spiega la DIM DS(2N) nella 110.
Detto questo, possiamo seguire in dettaglio come lavora il nostro Commodore: la prima volta che viene incontrata l’istruzione 130 è K=1, J=1 e il contenuto di tutti i vettori è … zero.
Nel Basic del C64, l’istruzione IF W THEN… equivale a IF W<>0 THEN… , questo significa che la IF nella 130 si incarica di controllare se “colonna – diagonale secondaria – diagonale principale” relative alla casella in gioco sono tutte “libere”: è sufficiente che anche uno solo dei tre valori non sia zero che si torna alla 130 dove J viene incrementato per la ricerca di una nuova casella “papabile”. All’inizio, però, C(..), DS(..) e DP(..) sono tutti nulli per cui non si torna alla 130. Sempre all’inizio è J=1 per cui la IF alla 140 non è verificata e il programma prosegue alla 150.
È qui che la regina viene posizionata (X(K)=J) e vengono impegnate la colonna (C(J)=1) e le diagonali.
All’inizio (K=1) è senz’altro K<N per cui, alla 150, K viene incrementato (si passa ad una nuova riga), J azzerato (cosicché, alla 130, J ripartirà da 1) e si torna alla 130 per un nuovo tentativo di posizionamento sulla linea successiva.
Come si diceva, per una linea fissata K, nella 130, l’indice J della colonna viene incrementato alla ricerca di una posizione accettabile per la regina. Se però J supera N, significa che nella riga in esame non si è trovata una posizione utile e occorre … fare un passo indietro. Alla 140 K viene decrementato (si torna indietro di una riga) e alla 210 l’indice di colonna viene riportato a quello relativo alla riga precedente (J=X(K)) e, quando poi si andrà alla 130, verrà aumentato di una unità alla ricerca di una nuova sistemazione. Contemporaneamente, sempre nella 210, vengono liberate la colonna e le diagonali da annullare.
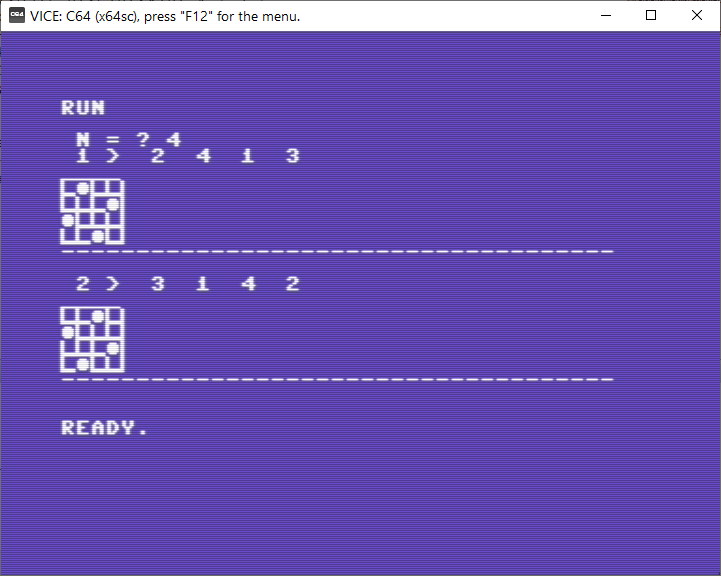
All’istruzione 160 si arriva solo quando K, l’indice di riga, raggiunge il valore N. In questo caso, le N regine hanno trovato una collocazione soddisfacente e si procede alla stampa: la variabile S, inizialmente posta uguale a 1, funge da contatore e contiene il numero della soluzione presentata, numero che viene stampato insieme al numero di colonna della regina per le varie righe. Il gruppo di istruzioni 170-200 si occupa della stampa della scacchiera. Alla 170 viene stampato il bordo superiore, poi, per ogni riga, si stampano X(T)-1 quadretti vuoti, quindi il carattere che rappresenta la regina (CHR$(113)), altri N-X(T) quadretti vuoti e il carattere CHR$(165) che completa l’ultima casella a destra in modo da ottenere la quadrettatura.
Il programma prosegue nella ricerca di altre soluzioni fino a quando, a furia di passi indietro, K non viene azzerato: tutte le soluzioni sono state trovate e stampate.
La pagina di Wikipedia “Rompicapo delle otto regine” è ricca di informazioni, in particolare viene segnalato il numero delle soluzioni al variare delle dimensioni della scacchiera. Provate il programma per N=5 e otterrete rapidamente le dieci soluzioni (in generale, il numero delle soluzioni cresce al crescere di N con un’eccezione: per N=6 le soluzioni sono quattro); con N=7 il C64 vi propone tutte le quaranta soluzioni.
Al crescere di N, il tempo di elaborazione può crescere a dismisura anche per ottenere la prima soluzione; il tempo dipende molto dal numero di “passi indietro” che il C64 è costretto a fare. Ad esempio, per N=12, l’emulatore VICE ha impiegato circa quattro minuti a trovare la prima delle 14200 soluzioni mentre per N=13 è bastato un minuto per trovare la prima delle 73712 soluzioni.
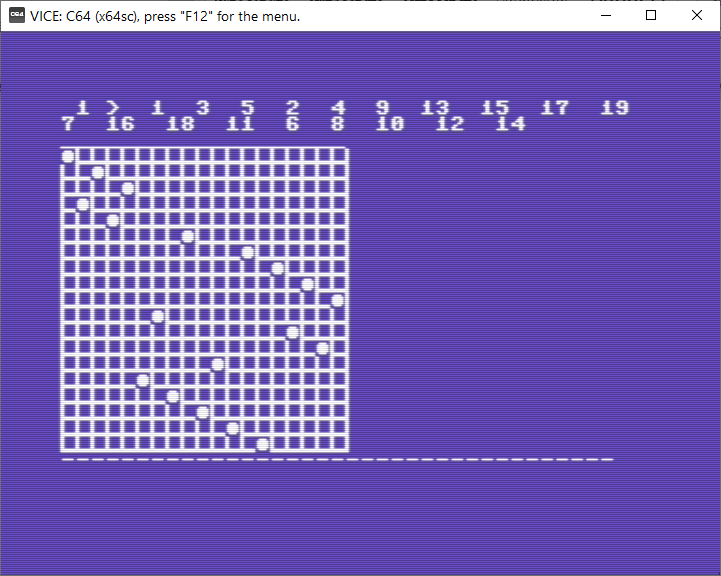
Ci sono voluti circa 50 minuti per ottenere la prima soluzione nel caso N=19 (caro C64, il tuo interprete Basic non è un campione di velocità, ma ti vogliamo bene lo stesso).
Vi sconsiglio il caso N=20 a meno di non far partire il C64 e partire poi per una vacanza alle Maldive…
Ancora due parole sull’algoritmo utilizzato: il backtrack. Come scrive Nicolò, si tratta di un esempio di “non soluzione”: non è un algoritmo costruito per lo specifico problema (ne esistono), semplicemente si passano in rassegna le “candidate soluzioni” (certo, in modo razionale ed ordinato), alla ricerca di quelle che soddisfano i vincoli richiesti. Questa “universalità” però è spesso controbilanciata da una… scarsa efficienza.
Per quanto riguarda il problema classico, N=8, Gauss trovò 72 soluzioni; il C64 trova tutte le 92 soluzioni in una ventina di minuti.
Risultato finale: Commodore 64 batte C.F. Gauss 92 a 72.
Scusate se è poco!
 |  |